




 in the top right corner
or press Esc) and select new game.
in the top right corner
or press Esc) and select new game. )
and click all the cells where you want to toggle pencil mark.
)
and click all the cells where you want to toggle pencil mark. )
and click all the cells where you want to erase contents. NOTE: It will erase numbers as well as pencil marks.
)
and click all the cells where you want to erase contents. NOTE: It will erase numbers as well as pencil marks. )
in the tool bar.
)
in the tool bar. )
in the tool bar.
)
in the tool bar.| Naked vs. Hidden Tuples Tuples is a mathematical concept - describing a set of elements. In case of Sudoku it refers to a set of candidates that appear in a certain set of cells. Usually in Sudoku we restrict it to a set of 1 (singles), 2 (doubles), 3 (triples) or 4 (quads). If X cells in a group contains X candidates (and no others) then those candidates can be safely removed from any other cells in that group. This combination called naked tuple. On the other hand there is a case when X candidates are restricted to X cells (that may contain other candidates as well). Any other candidates are invalid for those X cells and can be removed. This combination is called hidden tuples. Please review different example of naked and hidden doubles and triples that our puzzles can contain. |
|
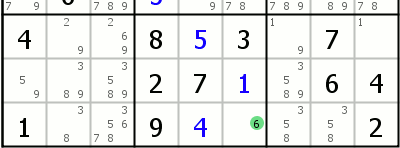 | Naked Singles The easiest strategy to explain - the cell may contain only one possible value. All other values are excluded because they already assigned to other cells in the group (row/column/box). |
 | Hidden Singles Certain option appears only in one cell in any particular group (row/column/box). That cell can contain other candidates, but no other cell in the group contains this option. In this example option 6 can only appear in one cell (column 4) in the last row on the image. |
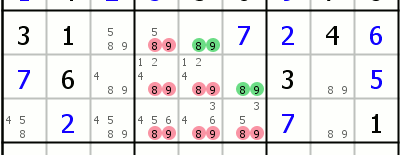 | Naked Doubles In this case you need to spot 2 cells that contain to same candidates (in the example - box containing 8 and 9). Since both of those values restricted to only those two cells, it means that no other cells in that group (box/line) can contain those values any more. |
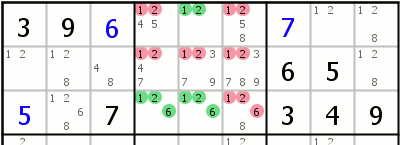 | Naked Triples Very similar to naked doubles. The thing to watch for is that not all 3 cells may contain identical candidates; some may contain only subset of possible values. In this example top row can contain only 1 and 2 whereas bottom row cells can contain 1,2 and 6. However only those 3 cells can contain any of those candidates. That means that no other cells in the box can have them. |
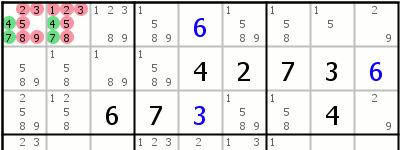 | Hidden Doubles Two candidates are restricted to 2 cells in the group. Those cells may contain other candidates but no other cells in the group contain those two candidates. That means that those two cells can't contain any other candidates. |
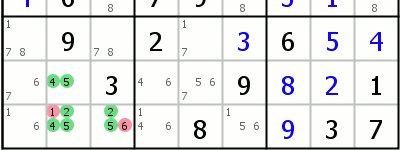 | Hidden Triples Similar to Hidden doubles - 3 possible candidates are restricted to 3 cells in the group. That means that no other candidates are allowed in those cells. |
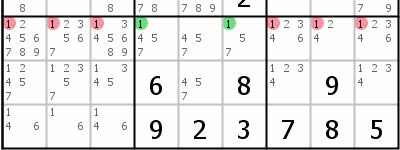 | Box/Line Reduction This technique refers to an intersection of box and line. When some option can't be found anywhere else in one of those intersecting groups, it is also invalid anywhere else outside the intersection in another group. In this example option 1 can be only found in the top row of the middle box. That means it's invalid anywhere outside middle box on the top row |
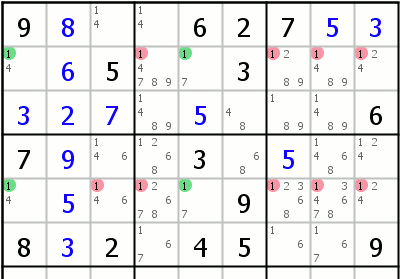 | Fish (X-Wing)/Swordfish/Jellyfish In this technique you need to find an option for 2 columns that only valid on intersection with 2 rows and nowhere else on those 2 columns, but valid somewhere else on those 2 rows (see example). In this case the option can be removed from any other place it is still valid on those two rows. The pattern can be transposed. In general case, any option if an option is only valid on 2 groups in intersection with other 2 groups, it can be removed from any cells in those 4 groups other than the intersections. The pattern can be applied for intersection of 3 groups with 3 other groups (Swordfish) or intersection of 4 groups with other 4 groups (Jellyfish). For additional detail on identifying and solving those techniques please check http://www.sudokuwiki.org/X_Wing_Strategy or http://hodoku.sourceforge.net/en/tech_fishb.php |
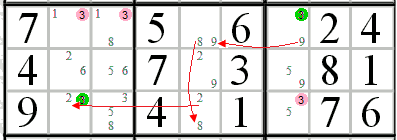 | XY Chain This is one of more complicated techniques. It deal with chains that connect bi-value cells - cells that only have 2 candidates and begins and ends on the same candidate. Then all the cells in the intersection of all possible groups in the beginning and ending cells of the chain can't contain this particular candidate. In the example we start the chain with candidate 3 in the R1C7, link it to candidate 9 in R1C7. From there we go to R1C5(9) -> R1C5(8) -> R3C5(2) -> R3C2(2) -> R3C2(3). As you see two consecutive links in our chain either share a cell or connect same candidate between two cells that belong to the same group. As a result, except for the R1C7 and R3C2, no other cells in either rows 1 and 3 and boxes 1 and 3 can contain candidate 3. For additional detail on identifying and solving those techniques please check http://www.sudokuwiki.org/XY_Chains or http://hodoku.sourceforge.net/en/tech_chains.php#xyc |
 | Nice Loops Nice loops is one of the more generic Sudoku solving techniques. Just like XY-Chain it involves identifying chains. Unlike XY-Chain it includes not only bi-value cells (cells that contain only 2 candidates) but also by-location cells (cells that have candidates that occur only twice in some group). Nice loops also need to start and end on the same cell. Then based on either odd or even number of nodes in the loop (continuous vs. discontinuous nice loops), either the beginning candidate is invalid or any other candidates are invalid. For additional detail on identifying and solving those techniques please check http://www.sudokuwiki.org/Alternating_Inference_Chains or http://hodoku.sourceforge.net/en/tech_chains.php#nl |